Cálculo numérico con bc
Marc Meléndez Schofield
Para la mayor parte de los cálculos numéricos que se pueden llegar a necesitar en el estudio de una carrera científica como ciencias físicas o matemáticas, no es necesario disponer de un ordenador potente, ni de software demasiado avanzado. Este artículo muestra cómo llevar a cabo cálculos relativamente interesantes con una simple calculadora de línea de comandos llamada bc.
bc viene instalado con la mayor parte de los sistemas inspirados en Unix (como Linux, FreeBSD, etc.). Tiene la ventaja de ser un programa sencillo y compacto, además del hecho de que los cálculos son interpretados (en otras palabras, no hace falta compilar). Sin embargo, tiene el inconveniente de ser un poco limitado (no se pueden crear matrices bidimensionales, por ejemplo).
Contenidos
- bc básico
- 1.1 Operaciones aritméticas
- 1.2 Variables
- 1.3 Funciones matemáticas
- Definición de funciones
- Creación de scripts
- 3.1 Condiciones
- 3.2 Bucles
- 3.2.1 for
- 3.2.2 while
- 3.2.3 Advertencia
- 3.3 Matrices
- 3.4 Variables auto
- 3.5 Instrucción read()
- 3.6 Pasar matrices por referencia
- Ejemplos
- 4.1 Matemáticas
- 4.1.1 Teoría de números
- 4.1.2 Probabilidad y estadística
- 4.1.3 Cálculo
- 4.1.4 Números complejos
- 4.1.5 Vectores
- 4.2 Física
- 4.2.1 Dinámica de una partícula
- 4.2.2 Campos de fuerzas
- 4.1 Matemáticas
1. bc básico
Para entrar en bc, simplemente ejecuta el comando bc desde la línea de comandos.
1.1 Operaciones aritméticas
A continuación, escribe 5+3 y pulsa enter.
> bc
5+3
8
La respuesta se muestra en la línea siguiente. Se pueden utilizar los paréntesis para agrupar términos.
(5+10)*2
30
5+10*2
25
Para calcular una potencia, se utiliza el signo ^.
2^5
32
La división puede resultar desconcertante en un primer momento.
7/5
1
Esto es debido a que en la solución se están ignorando los decimales. Por defecto, obtenemos el cociente entero. El resto de la división se puede calcular con el operador %.
7%5
2
El número de decimales de los cálculos se controla con la variable scale. Si queremos dos decimales,
scale=2
7/5
1.40
La raíz cuadrada se calcula con la función sqrt (del inglés "square root").
sqrt(4)
2
Para salir del programa, escribe quit y pulsa enter.
1.2 Variables
Vamos a suponer que queremos calcular la solución del problema siguiente:
Calcular la fuerza eléctrica que ejerce una carga de 1 microcoulombio sobre una carga de 2,5 microcoulombios situada en el vacío a 5 centímetros de ella.
Podríamos aplicar la ley de Coulomb (F = K(q1·q2)/r2),
scale=7
9*10^9*1*10^-6*2.5*10^-6/0.05^2
9.0000000
pero es más legible definir los valores por separado, y utilizar una expresión simbólica (nótese que las variables se representan con letras minúsculas).
scale = 7
k = 9*10^9
q1 = 1*10^-6
q2 = 2.5*10^-6
r = 0.05
k*q1*q2/r^2
9.0000000
También se podría haber definido la variable f, así:
f = k*q1*q2/r^2
f
9.0000000
Hay que tener cuidado con las expresiones del tipo "3a", que devuelven un mensaje de error. Los productos se deben escribir explícitamente: 3*a.
a=3
3a
(standard_in) 21: syntax error
3*a
9
1.3 Funciones matemáticas
Si, en lugar de ejecutar el comando bc a secas, se utiliza la opción -l (es decir, escribimos el comando bc -l), bc carga su librería matemática, que incluye las funciones seno, coseno, arco tangente, logaritmo natural, exponencial y de Bessel.
Podemos calcular los logaritmos neperianos de 1 y 2 así:
> bc -l
l(1)
0
l(2)
.69314718055994530941
Las funciones incluídas en la librería matemática son:
- s(x) Seno de x (x en radianes).
- c(x) Coseno de x (x en radianes).
- a(x) Arco tangente de x, (devuelve un valor en radianes).
- l(x) Logaritmo natural x.
- e(x) Exponencial de x.
- j(n,x) Función de Bessel de orden n en x.
2. Definición de funciones
El lector habrá notado, quizás, que no se mencionó la función tangente entre las de la librería matemática de bc. Esto se debe, simplemente, a que bc no incluye esta función por defecto. Sin embargo, esto es muy fácil de remediar con conocimientos básicos de trigonometría. En efecto, podríamos calcular la tangente de π/4 radianes de la siguiente manera.
> bc -l
pi = 3.1415927;
s(pi/4)/c(pi/4);
1.00000002320510365001
quit
El resultado no es exactamente 1 debido a que sólo hemos utilizado siete decimales en la expresión de π.
Supongamos que queremos calcular la tangente de muchos ángulos diferentes. En este caso, sería mucho más sencillo tener una función tangente (t(x), por ejemplo) en lugar de tener que invocar el cociente entre el seno y el coseno. Podemos definir esta función de la manera siguiente:
> bc -l
pi=3.1415927;
define t(x) {return s(x)/c(x);}
t(pi/4);
1.00000002320510365001
t(pi/6);
.57735027950300509089
Hemos creado la función t(x) con la instrucción define. Entre llaves, explicamos el efecto de la función, que toma un valor (representado por x) y devuelve el seno de este valor dividido por su coseno (s(x)/c(x)). Algunas versiones de bc pueden exigir que lo que sigue al return vaya entre paréntesis.
Evidentemente, sería mucho más cómodo poder definir la función tangente de una vez por todas. ¿Y por qué limitarnos a la función tangente y no incluir también el valor de otras funciones, como la secante, o incluso el valor de π? Para ello, escribimos en un archivo de texto las instrucciones siguientes:
pi=3.1415927;
define t(x) {
return s(x)/c(x);
}
define sec(x) {
return 1/c(x);
}
define cosec(x) {
return 1/s(x);
}
define cotan(x) {
return c(x)/s(x);
}
Podemos guardar las líneas precedentes en "trigonometria.bc". Ya no es necesario incluir la definición de una función en una sola línea, y esto hace más legibles nuestros cálculos.
Cuando queramos utilizar nuestras definiciones, basta con incluir el nombre de nuestro archivo al invocar bc. Es importante recordar que si estamos ejecutando bc desde un directorio diferente del que contiene nuestro archivo, es necesario incluir también la ruta hasta el archivo.
> bc -l trigonometria.bc
cosec(pi/6);
1.99999997320505505194
3. Creación de scripts
Hasta ahora, hemos visto cómo definir funciones que utilizaremos más adelante en nuestros cálculos, pero siempre hemos sido nosotros quienes debíamos indicar la operación a llevar a cabo. Esto no es una exigencia de bc. No hay ningún problema si también queremos incluir cálculos definidos de antemano en nuestros ficheros.
Supongamos que necesitamos los cien primeros decimales del número π. Como sabemos que tg(π/4) = 1, podemos deducir que π = 4 arctg(1). Recuérdese que la función arctg(x) se expresa en bc como a(x).
En el fichero pi.bc podríamos escribir esto:
/* Los cien primeros decimales de pi */
scale = 100;
print "Cálculo de pi hasta el centésimo decimal:\n";
print 4*a(1);
print "\n";
quit;
La expresión entre los signos /* y */ es un comentario, y bc se lo salta al interpretar nuestras instrucciones. Los comentarios se incluyen para que el código sea más legible, no sólo por otros programadores, sino también para uno mismo. Un programa complejo sin comentarios se vuelve completamente ilegible en cuanto uno lo ha dejado de lado durante una temporada.
Volvamos a nuestro código. La instrucción scale indica que realizaremos cálculos de cien decimales. Print muestra un mensaje en pantalla. El signo "\n" indica un retorno, es decir, el texto pasa a la siguiente línea, y "quit" sale del programa. La instrucción "print 4*a(1);" muestra en pantalla el cálculo deseado. Como la función arco tangente viene incluída en la librería matemática, es necesario ejecutar el programa con la opción "-l".
> bc -l pi.bc
Cálculo de pi hasta el centésimo decimal:
3.141592653589793238462643383279502884197\
16939937510582097494459230781640628620899\
86280348253421170676
3.1 Condiciones
Vamos a definir una función que calcule el factorial de un número. El lector recordará que n! (factorial de n, siendo n un número natural) se define como
n! = n·(n-1)!
Es decir, el factorial de un número es igual a este número multiplicado por el factorial de este número menos uno. Esto es un ejemplo típico de definición recursiva (es decir, que incluye el mismo término a definir). Si definimos 0! = 1 (para garantizar que el cálculo finalice en algún momento), podemos definir el factorial en bc como sigue:
/* Factorial de un número natural*/
scale = 0;
define factorial(n) {
if(n < 0)
print "Error: Factorial de un número negativo no definido.\n";
if(n == 0)
return 1;
if(n > 0)
return n*factorial(n-1);
}
Este código incluye varias condiciones. Si n es negativo, entonces se muestra un mensaje de error. En el caso de que n sea igual a cero, la función devuelve 1. Para números naturales positivos, utilizamos la definición recursiva.
Nótese que se utilizan dos signos de igual para expresar la igualdad entre n y cero. El operador = se conoce como operador de asignación (asigna a una variable un valor). Por ejemplo, "x = 3" asigna a la variable "x" el valor 3. "x == 3" devuelve 1 (verdadero) si "x" es efectivamente igual a 3 y 0 (falso) en caso contrario.
> bc
a = 3;
a == 3;
1
a = 2;
a == 3;
0
Supongamos que el código definido más arriba se ha incluido en el fichero factorial.bc:
> bc -l factorial.bc
factorial(5);
120
factorial(-2);
Error: Factorial de un número negativo no definido.
factorial(120);
66895029134491270575881180540903725867527463331380\
29810295671352301633557244962989366874165271984981\
30815763789321409055253440858940812185989848111438\
9650005964960521256960000000000000000000000000000
3.2 Bucles
3.2.1 for
También podríamos haber definido la función factorial mediante un bucle. n! es el producto desde 1 hasta n.
n! = 1·2···(n-1)·n
En código:
/* Función factorial (con bucle for) */
scale = 0;
define factorial (n) {
resultado = 1;
for(i = 1; i <= n; i++)
resultado *= i;
return resultado;
}
Este algoritmo es más lento que el recursivo.
Los resultados parciales se guardan en la variable resultado (que empieza valiendo 1). La instrucción for funciona así:
for(<inicialización>;<condición>;<actualización>)
La inicialización es una instrucción que se ejecuta antes de que comience el bucle. En nuestro caso, se asigna el valor 1 a la variable i. La condición se evalúa en cada repetición. Si la condición se cumple (aquí, que i es menor o igual que n) entonces se vuelve a ejecutar la instrucción que sigue al for. La actualización se ejecuta después de cada repetición. La actualización que usamos aquí es i++, que es una manera de aumentar i en una unidad. Es decir, i++ es equivalente a i = i + 1. En cada iteración (repetición), se ejecuta el comando
resultado *= i;
que es otra forma de escribir
resultado = resultado * i;
Finalmente, se devuelve la variable resultado.
3.2.2 while
Otra opción para programar bucles es utilizar un bucle while. Veamos un ejemplo.
/* Función factorial (bucle while) */
scale = 0;
define factorial(n) {
i = 1;
resultado = 1;
while (i <= n)
{
resultado *= i;
i++;
}
return resultado;
}
Este algoritmo es sólo ilustrativo. Desde el punto de vista del cálculo de un factorial no es demasiado bueno.
Este programa también incluye la utilización de las llaves para agrupar instrucciones. A continuación de la instrucción while hay un bloque de instrucciones entre llaves. El comando while se aplica al bloque entero.
3.2.3 Advertencia
Con los bucles siempre hay que asegurarse de que la condición de salida del bucle se cumplirá en algún momento. De otra forma, entraremos en un bucle infinito. Por ejemplo, la siguiente función se ejecuta indefinidamente.
/* Bucle infinito */
define bucleinfinito(x) {
while(1<2)
{
print x++;
print ": ¡Socorro! Estoy en un bucle infinito.\n";
}
}
Para salir de un bucle infinito mientras se está ejecutando pulsa CTRL+C.
3.3 Matrices
bc permite definir matrices de una dimensión. El índice de cada elemento se encierra entre paréntesis. Podemos definir el vector v = (1, -1, 2) y calcular su módulo así:
scale = 5;
v[1] = 1 ; v[2] = -1; v[3] = 2;
sqrt(v[1]^2 + v[2]^2 + v[3]^2);
2.44948
Una función puede aceptar una matriz como argumento. Veremos un ejemplo en el que definimos el sumatorio de los n primeros elementos almacenados en una matriz.
define sumatorio(x[], n) {
suma = 0;
for(i = 1; i <= n; i++)
suma += x[i];
return suma;
}
Los corchetes en x[] indican que la variable x es una matriz. suma += x[i] es equivalente a escribir suma = suma + x[i]. Nótese que se recorren los índices de la matriz x con la variable i (que cambia en cada iteración del bucle). Sigue un ejemplo de utilización de la función sumatorio.
u[1] = 1; u[2] = 5; u[3] = 7; u[4] = 5;
sumatorio(u[], 4);
18
sumatorio(u[], 2);
6
3.4 Variables auto
Supongamos que tenemos una función contar(n) que muestra en pantalla los números desde 1 hasta n.
define contar(n) {
for(i = 0; i <= n; i++)
print i, " ";
print "\n";
}
Esta función no devuelve explícitamente ningún valor (nótese la ausencia de la instrucción return). bc presupone en estos casos que el valor devuelto es cero. Al invocar la rutina, se mostrará este valor nulo en la pantalla.
contar(5);
1 2 3 4 5
0
Para evitar este cero no deseado, podemos asignar el valor devuelto a una variable. bc permite asignar valores al punto (.), que no suele usarse como nombre de variable.
. = contar(5); 1 2 3 4 5
Imaginemos que queremos utilizar nuestra función para mostrar números dispuestos así:
1
1 2
1 2 3
1 2 3 4
1 2 3 4 5
Si escribimos esto,
for(i = 0; i <= 5; i++)
. = contar(i);
obtenemos el resultado siguiente:
1
1 2 3
1 2 3 4 5
¿Dónde están las dos líneas que faltan? El problema aquí es que la función contar(n) también cambia el valor de la variable i.
La solución, dirá el lector, es utilizar una variable distinta para cada bucle. Y tiene razón, pero hay un problema. Puede que contar(n) la haya escrito una persona y que la esté utilizando otra, que no tiene por qué saber los nombres de las variables que usa esta función. Para usarla, debería bastar con saber qué hace, sin tener que consultar cómo lo hace. bc permite usar la instrucción auto para especificar que una variable es propia de una función.
define contar(n) {
auto i;
for(i = 0; i <= n; i++)
print i, " ";
print "\n";
}
De este modo, bc sabe que la "i" utilizada dentro de contar es diferente de cualquier otra que se haya podido utilizar en el programa.
Este bloque termina con una advertencia importante. Si la función contar invocara a otra función que utilizara la variable i (y que no tuviera instrucción auto), entonces la variable modificada sería la de contar(n), y no la de otras partes del programa. Es decir, las variables auto forman una jerarquía. Si en una función f no se declara que una variable es auto, entonces la variable a la que nos referimos es la de la función que invocó a f (que a su vez puede ser la de la función que invocó a esta, y así sucesivamente hasta que encontremos una declaración auto, o ninguna, en caso de que siempre nos estemos refiriendo a la misma variable).
3.5 Instrucción read()
En algunas ocasiones, puede resultar conveniente que ciertos datos se introduzcan durante la ejecución de la función. Para ello, se utiliza la instrucción read().
define pi() {
auto s, n, pi;
s = scale;
print "Decimales de pi:\n";
n = read();
scale = n;
pi = 4*a(1);
scale = s;
return pi;
}
Al invocar la función pi() obtenemos lo siguiente (los valores 10 y 20 los introduce el usuario):
pi();
Decimales de pi:
10
3.1415926532
pi();
Decimales de pi:
20
3.14159265358979323844
3.6 Pasar matrices por referencia
Puede que necesites que una función cambie el valor de uno de sus argumentos. Por ejemplo, si tenemos una matriz que guarda los datos de una hora (horas, minutos y segundos) y queremos añadir h horas, m minutos y s segundos, podemos usar la función siguiente:
define sumahoras(*hora[], h, m, s) {
s = scale;
scale = 0;
hora[1] = hora[1] + h + (hora[2] + m)/60 + (hora[3] + s)/3600;
hora[2] = (hora[2] + m + (hora[3] + s)/60)%60;
hora[3] = (hora[3] + s)%60;
scale = s;
}
El asterisco delante de la matriz hora[] en la primera línea de la definición indica que la matriz se pasa por referencia. Si no se incluye este asterisco, la función no modifica la matriz hora[], sino una copia local de estas variables.
El resultado es éste:
/* Hora original: 1:20:45 */ mihora[1] = 1; mihora[2] = 20; mihora[3] = 45; /* Suma 2 horas, 45 minutos y 20 segundos */ . = sumahoras(mihora[], 2, 45, 20); /* Resultado */ print mihora[1], ":", mihora[2], ":", mihora[3], "\n"; 4:6:5
Si no hubiéramos pasado la matriz mihora[] por referencia, nos habríamos encontrado que el resultado era 1:20:45.
4. Ejemplos
El código de los ejemplos que siguen debería poder consultarse en mi espacio gopher, junto a este archivo.
(gopher://sdf.lonestar.org/1/users/marcmmw/esp/programacion)
En esta versión (html), he incluído un enlace directo a cada uno de los ficheros. Los usuarios de Firefox deberían poder acceder sin problemas utilizando el complemento Overbite. Los usuarios de Internet explorer pueden descargar Firefox gratuitamente en la página oficial de firefox.
4.1 Matemáticas
En los siguientes ejemplos, se comentan sólo fragmentos de código. Con el signo [...] se indica la omisión de alguna parte del programa.
4.1.1 Teoría de números (numeros.bc)
Nuestro ejemplo incluye un algoritmo para encontrar los factores primos de un número natural n. No es el algoritmo más eficiente, pero es uno de los más sencillos de comprender.
Para cada número i menor que n, comprobamos si n es divisible entre i, es decir, si el resto de n entre i es cero. Si es así, realizamos la división y factorizamos el cociente. Con este método, sólo es necesario que i recorra los números desde 2 hasta la raíz cuadrada de n (el lector puede entretenerse en demostrar esto).
/* Factores primos */
define factores(n) {
[...]
if(n >= 2)
{
m = n;
i = 2;
while(i <= sqrt(n))
{
if((m % i) == 0)
{
[...]
print i;
m = m / i;
i = i - 1;
}
i = i + 1;
}
}
[...]
}
El fichero contiene también funciones que calculan los n-ésimos números de Mersenne y de Fermat.
> bc -l numeros.bc
factores(1254);
2, 3, 11, 19.
1254
mersenne(12);
4095
fermat(5);
65537
factores(fermat(4));
65537.
65537
factores(mersenne(12));
3, 3, 5, 7, 13.
4095
También se puede utilizar la función comb(n,m) para calcular números combinatorios (coeficientes binomiales). El triángulo de Tartaglia (también conocido como triángulo de Pascal) se consigue ordenando los coeficientes binomiales por filas, de modo que cada número es igual a la suma de los dos números más cercanos en la fila inmediatamente superior.
1 1
1 2 1
1 3 3 1
1 4 6 4 1
etc.
Mediante comb(n,m) es muy sencillo calcular los coeficientes del triángulo por filas, como veremos a continuación. Mediante un bucle (en i) se recorren las filas del triángulo. En cada iteración de este bucle, se ejecuta otro bucle (en j) que comienza en 0 y acaba en el valor que toma i en la iteración, para recorrer todos los elementos de la fila. Se muestra cada elemento en pantalla (separándolo del anterior con un espacio). Nótese que antes se ha introducido un bucle en j para imprimir un número adecuado de espacios antes de los elementos de una fila para crear el hueco a la izquierda del triángulo.
> bc -l probabilidad.bc
scale = 0;
for(i = 1; i <= 9; i++)
{
/* Deja hueco a la izquierda de la fila */
for(j = 1; j <= 9 - i; j++)
print " ";
/* Muestra en pantalla los coeficientes */
for(j = 0; j <= i; j++)
print comb(i,j), " ";
/* Pasa a la línea siguiente */
print "\n";
}
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
El cálculo está resuelto, pero la alineación todavía no es perfecta. El lector ambicioso querrá, quizás, ensayar soluciones más sofisticadas.
Leo en la wikipedia que si se marcan los números impares del triángulo de Tartaglia, se obtiene una figura parecida al triángulo de Sierpinski. Vamos a comprobarlo cambiando el segundo bucle en j del código anterior por las líneas siguientes.
for(j = 0; j <= i; j++)
{
if(comb(i,j)%2==1) print "X ";
if(comb(i,j)%2==0) print " ";
}
En la prueba que hice yo, dibujé las primeras quince filas (en lugar de nueve) y empecé en i = 0. El resultado es un dibujo como el que se muestra a continuación.
X
X X
X X
X X X X
X X
X X X X
X X X X
X X X X X X X X
X X
X X X X
X X X X
X X X X X X X X
X X X X
X X X X X X X X
X X X X X X X X
X X X X X X X X X X X X X X X X
Con más líneas el parecido es todavía más evidente.
4.1.2 Probabilidad y estadística (probabilidad.bc)
Las funciones de densidad de probabilidad dependen de la librería matemática.
En probabilidad.bc se definen funciones para calcular la media aritmética y la desviación estándar de n datos almacenados en una matriz.
> bc -l probabilidad.bc
scale = 2;
x[1] = 2; x[2] = 4; x[3] = 4; x[4] = 4;
x[5] = 5; x[6] = 5; x[7] = 7; x[8] = 9;
media(x[], 8);
5.00
desv(x[], 8);
2.00
¿Qué más incluye el fichero probabilidad.bc? Además de las funciones factorial y comb(n,m), se encuentran definidas las funciones binomial, normal y de Poisson utilizadas en probabilidad y estadística.
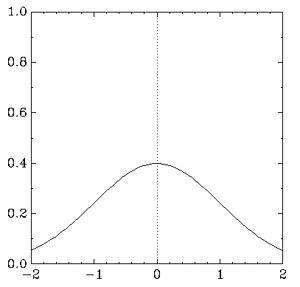
Figura 1: Distribución normal con μ = 0 y σ = 1.
Con la función norm(x, mu, sigma) se obtuvieron los datos para crear la gráfica de la función normal con mu = 0 y sigma = 1 (ver figura 1).
Para crear un gráfico como este es necesario, en primer lugar, calcular los datos (en nuestro caso, con bc). A continuación se utiliza un programa de dibujo (la figura 1 se creó con graph, incluido en los plotutils).
Para el primer paso, se calculan los valores de muchas parejas de valores (x, f(x)). Por ejemplo, se pueden escribir las siguientes líneas en un fichero normal.bc:
scale = 10;
for(x = -2; x <= 2; x += 0.05)
print x, " ", norm(x,0,1), "\n";
quit
La rutina anterior calcula el valor de la función norm para valores de x entre -2 y 2 separados por intervalos de 0.05. Ejecutando esta rutina junto con el contenido de probabilidad.bc obtenemos los datos.
> bc -l probabilidad.bc normal.bc
-2 .0539909664
-1.95 .0595947060
-1.90 .0656158147
[...]
1.90 .0656158147
1.95 .0595947060
2.00 .0539909664
Se podrían copiar todos estos datos a mano, o cortando y pegando, pero es mucho más cómodo redirigirlos a un fichero (aquí normal.dat) directamente desde la línea de comandos así:
> bc -l probabilidad.bc normal.bc > normal.dat
En lugar de mostrar los datos en pantalla, la instrucción "> normal.dat" indica que los datos deben guardarse en el fichero nombrado.
Ahora queremos crear una imagen a partir de estos datos con el programa graph.
> graph -T gif -y 0 1 normal.dat > normal.gif
Con "-T gif" se especifica el formato de la imagen. "-y 0 1" indica el rango de valores del eje y. Si se instala plotutils, se suelen instalar también las páginas de manual correspondientes, por lo que pueden consultarse ahí más opciones del comando graph. La página del manual se invoca así:
> man graph
Pueden conseguirse los mismos resultados de manera más sencilla con programas como gnuplot, pero uno de los objetivos de este artículo es el de mostrar cómo se pueden realizar cálculos relativamente sofisticados con recursos muy limitados.
4.1.3 Cálculo (calculo.bc)
Este apartado está dedicado a la derivación e integración numérica, pero comentaremos antes el cálculo numérico de límites. En los casos en los que no existe indeterminación, basta con sustituir el valor correspondiente. Para calcular el límite
sin(x)
lim -------
x -> 2 2 Ln(x)
no hay más que escribir
> bc -l
s(2)/(2*l(2))
El problema surge con los límites en el infinito y las indeterminaciones. Veamos el límite de sin(x)/x en x = 0.
> bc -l
s(0)/0
Runtime error (func=(main), adr=7): Divide by zero
La idea intuitiva que hay detrás de la definición matemática de límite de una función en un punto es ésta: a medida que la variable se aproxima al punto considerado, el valor de la función se aproxima inexorablemente al límite (si es que existe). Por lo tanto, podemos examinar el comportamiento de la función en las cercanías del punto.
> bc -l
s(0.1)/0.1
.99833416646828152300
s(0.01)/0.01
.99998333341666646800
s(0.001)/0.001
.99999983333334166000
El límite en este caso parece ser igual a uno (y, de hecho, lo es).
Para los límites en el infinito, podemos utilizar valores grandes en valor absoluto.
> bc -l
e(-10)
.00004539992976248485
e(-20)
.00000000206115362243
e(-50)
0
Evidentemente, lo que cuenta como número "grande" depende del contexto.
En cualquier caso, podríamos preguntar qué garantía tenemos de que la función vaya a respetar la tendencia observada para entornos más reducidos (o números mayores). La respuesta es que, sin una demostración rigurosa, no hay garantía, y es importante tener en cuenta este hecho en la derivación e integración numéricas (cuyas definiciones están basadas, al fin y al cabo, en la de límite). El lector puede entretenerse en intentar determinar (sin éxito) el límite de sin(1/x) cuando x tiende a cero, por el método indicado.
Sin embargo, si las funciones tienen un comportamiento suficientemente parecido al de una recta en los intervalos considerados, es fácil definir una aproximación numérica para sus derivadas e integrales. La definición de derivada es:
f(a + h) - f(a)
f'(a) = lim ---------------
h -> 0 h
Para conseguir una aproximación, bastará con calcular el cociente sustituyendo h por un valor p suficientemente pequeño. Por ejemplo, la derivada de sin(x) en x = 0 se puede aproximar así:
> bc -l
(s(0 + 0.01) - s(0))/0.01
.99998333341666646800
Como siempre, nos gustaría tener una función que tome la función a derivar, el punto, y el paso p. Pero en bc no se pueden pasar las funciones como parámetros, es decir, no se puede definir una función derivada(f(x), x, p), siendo f otra función. Afortunadamente, podemos resolver este problema dando un pequeño rodeo.
define derivada(a,p) {
return (f(a+p) - f(a))/p;
}
En calculo.bc la función derivada asume que la función a derivar se llama f(x), por lo que sólo hay que definirla antes de invocar la rutina.
> bc -l calculo.bc
pi = 3.1415927;
/* Ahora la función a derivar es sin(x) */
define f(x) { return s(x);}
derivada(pi/6,0.0001);
.8660010000
/* Ahora la función a derivar es cos(x) */
define f(x) { return c(x);}
derivada(pi/6,0.0001);
-.5000430000
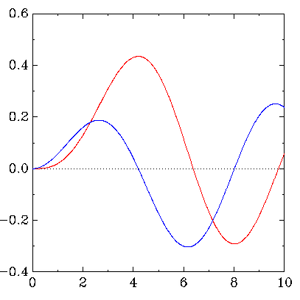
Figura 2: Función de Bessel de orden 3 (en rojo) y su derivada (en azul). Datos calculados con bc y dibujados con graph.
En nuestro fichero hemos incluido también la derivada enésima por medio de una definición recursiva.
Podemos utilizar nuestra rutina para calcular derivadas laterales, lo cual es especialmente útil en funciones definidas por intervalos.
> bc -l calculo.bc
define f(x) {
if(x <= 0) return x^2;
if(x > 0) return x;
}
/* Derivada de f(x) en cero por la derecha */
derivada(0, 0.001);
1.0000000000
/* Derivada de f(x) en cero por la izquierda */
derivada(0, -0.001);
-.0010000000
Para calcular las integrales, utilizaremos la definición de Riemann.
/ b __ N
| f(x) dx = lim > f(x ) h
/ a h -> 0 ~~i = 0 i
Donde N = (a + b)/h. De nuevo, aproximamos el límite sustituyendo h por un valor pequeño p y obteniendo un sumatorio finito.
define integral(a, b, p) {
integ = 0;
for(x = a; x < b; x += p)
integ += f(x)*p;
return integ;
}
Para calcular la integral definida de la función cos(x) entre π/2 y π:
> bc -l calculo.bc
pi = 3.1415927;
define f(x) { return c(x);}
integral(pi/2, pi, 0.01);
-1.0041953600
Para conseguir una aproximación mayor se puede utilizar un paso menor, pero hay ocasiones en que es conveniente utilizar un número más reducido de pasos (por ejemplo, cuando el tiempo que lleva evaluar la función f(x) es elevado). Nuestra aproximación medía el área bajo la curva f(x) con rectángulos, pero podemos cambiar el borde superior de nuestros rectángulos para que se ajuste más a la curva f(x) como, por ejemplo, si utilizamos una recta desde el punto (x, f(x)) al punto (x + h, f(x + h)). Hemos introducido una aproximación todavía mejor mediante tramos parabólicos atribuida a Thomas Simpson.
> bc -l calculo.bc
scale = 20;
pi = 4*a(1);
define f(x) { return s(x);}
integral(0, 2*pi, 0.1);
-.00069944923028496906
simpson(0, 2*pi, 0.1);
.00014136362149477784
4.1.4 Números complejos (complejos.bc)

Figura 3: Fractal de Mandelbrot y
detalle del mismo (derecha).
Los cálculos se realizaron en
bc con las rutinas de complejos.bc.
En este apartado se ponen de manifiesto algunas de las limitaciones de bc. Las funciones no pueden devolver matrices (es decir, no es válida la instrucción return z[];), así que hay que buscar algún sistema alternativo.
Representaremos los números complejos con una matriz de dos elementos, de modo que si z = a + bi, usaremos las asignaciones siguientes:
z[0] = a;
z[1] = b;
Algunas funciones devuelven un número real (parte real, parte imaginaria, módulo y argumento), mientras que otras deberían devolver un número complejo (exponencial de un número complejo, por ejemplo). En estos últimos casos, pasaremos por referencia la matriz donde queremos que se almacene la acción de la función, mientras que la función devolverá el valor cero.
En nuestro ejemplo, definiremos dos números complejos z1 = 3 + 2i, y z2 = -1 + i. Podemos mostrarlos en forma de binomio con la rutina printz(z[]).
z1[0] = 3; z1[1] = 2;
z2[0] = -1; z2[1] = 1;
. = printz(z1[]);
3 + 2i
. = printz(z2[]);
-1 + 1i
Asignamos el valor de la función print z a la variable "." para evitar que se muestre en pantalla un cero adicional (ver sección 3.4). A continuación, Al sumar, restar, multiplicar o dividir z1 y z2, guardamos el resultado la variable zres[].
. = sumaz(z1[], z2[], zres[]); . = printz(zres[]);
2 + 3i
. = restaz(z1[], z2[], zres[]); . = printz(zres[]);
4 + 1i
. = prodz(z1[], z2[], zres[]); . = printz(zres[]);
-5 + 1i
scale = 2;
. = divz(z1[], z2[], zres[]); . = printz(zres[]);
-0.50 + -2.50i
Podemos calcular la parte real, imaginaria, módulo y argumento. La función printzt(z[]) escribe z en forma trigonométrica.
rez(z1[]);
3
imz(z1[]);
2
modz(z1[]);
3.60
argz(z1[]);
.58
. = printzt(z1[]);
3.60 * (cos(.58) + i sin(.58))
Las potencias en bc sólo aceptan exponentes enteros, así que he definido una función pot(x, y) para exponentes reales arbitrarios. Utilizando esta expresión, he escrito otra llamada potz que calcula el resultado de elevar un número complejo a un número real arbitrario. pot(x,y) utiliza el operador ^ cuando y es entero, y la expresión
xy = ey Ln(x)
para cualquier otro número real.
scale = 5;
/* Cálculo de 3^2.1 */
pot(3,2.1);
10.04505
/* Cálculo de z1^2.1 */
. = potz(z1[], 2.1, zres[]); . = printz(zres[]);
4.87294 + 13.95202i
Se puede calcular una raíz de orden n utilizando potz para hallar la potencia 1/n. El resto de las raíces se pueden ir calculando multiplicando este resultado por e2πki/n, con k = 1, 2, ..., n - 1. La función raices(z[],n) muestra n raíces de z[].
z[0] = 1; z[1] = 0;
/* Raíz octava de 1 */
. = potz(z[], 1/8, zres[]); . = printz(z[]);
1 + 0i
/* Ocho raíces octavas de 1 */
. = raicesz(z[], 8);
1.00000 + 0i
.70711 + .70710i
0 + 1.00000i
-.70710 + .70710i
-.99999 + 0i
-.70710 + -.70710i
0 + -1.00000i
.70710 + -.70711i
El fichero incluye también funciones para calcular exponenciales, senos, cosenos y logaritmos de números complejos. Como el logaritmo es una función multivaluada, logz(z[], zres[]) almacena en zres[] solamente uno de los valores posibles. Los demás pueden hallarse sumando 2πki a este valor (donde k es un número entero). Por último, la función potzz(z1[],z2[], zres[]) calcula el resultado de z1z2.
. = expz(z1[], zres[]); . = printz(zres[]);
-8.35839 + 18.26357i
. = sinz(z1[], zres[]); . = printz(zres[]);
.53087 + -3.59055i
. = cosz(z1[], zres[]); . = printz(zres[]);
-3.72452 + -.51178i
. = logz(z1[], zres[]); . = printz(zres[]);
1.28247 + .58799i
. = potzz(z1[], z2[], zres[]); . = printz(zres[]);
.22950 + 3.65836i
4.1.5 Vectores (vectores.bc)
Utilizando ideas parecidas a las de la sección anterior, se pueden definir las operaciones vectoriales. Las funciones que devuelvan un vector almacenarán su resultado en la variable vres[]. La función printv(v[]) muestra el vector v[] con sus coordenadas listadas entre paréntesis. Las funciones están definidas para vectores tetradimensionales, pero se pueden utilizar para vectores en dos y tres dimensiones dejando las componentes adicionales iguales a cero:
v[1] = 1; v[2] = -1;
Con este comando se define el vector v = (1, -1). bc supone automáticamente que v[0] y v[3] son nulos (siempre que no se les haya asignado antes un valor diferente).
Definiremos los vectores v1 = (0, 2, -1, 2), v2 = (-1, 1, 0, 3) y v3 = (0, 0, 2, -1).
v1[0] = 0; v1[1] = 2; v1[2] = -1; v1[3] = 2;
v2[0] = -1; v2[1] = 1; v2[2] = 0; v2[3] = 3;
v3[0] = 0; v3[1] = 0; v3[2] = 2; v3[3] = -1;
. = printv(v1[]); . = printv(v2[]); . = printv(v3[]);
(0, 2, -1, 2)
(-1, 1, 0, 3)
(0, 0, 2, -1)
A continuación se muestran ejemplos de las operaciones de suma, resta y producto por un escalar.
/* Suma de vectores */
. = sumav(v1[], v2[], vres[]); . = printv(vres[]);
(-1, 3, -1, 5)
/* Resta de vectores */
. = restav(v1[], v2[], vres[]); . = printv(vres[]);
(1, 1, -1, -1)
/* Producto por un escalar */
. = prodv(3, v1[], vres[]); . = printv(vres[]);
(0, 6, -3, 6)
Sigue un ejemplo de los productos internos. El producto escalar y el producto mixto devuelven un número real, por lo que no es necesario consultar el valor de vres[] después de invocar estas funciones. El producto vectorial y el producto mixto están definidos para vectores tridimensionales, por lo que no entra en el cálculo la primera componente de los vectores (la de índice 0).
/* Producto escalar */
escalar(v1[], v2[]);
8
/* Producto vectorial (Para vectores tridimensionales) */
. = vectorial(v1[], v3[], vres[]); . = printv(vres[]);
(0, -3, 2, 4)
/* Producto mixto (Para vectores tridimensionales) */
mixto(v1[], vres[], v3[])
-13
4.2 Física
Es relativamente común encontrarse en física con una ecuación intratable desde el punto de vista analítico. En estos casos, no queda más remedio que recurrir a una solución numérica.
4.2.1 Dinámica de una partícula (fuerzas.bc)
La idea básica para resolver las ecuaciones del movimiento de una partícula sometida a fuerzas es sencilla. Se parte de las ecuaciones de Newton,
F = m · a,
y despejando la aceleración,
a = d2r/dt2 = F/m.
Las derivadas se calculan de forma aproximada utilizando incrementos temporales pequeños (en lugar de resolver el límite de la definición).
df f(t + h) - f(t) ~ f(t + dt) - f(t)
-- = lim --------------- = ----------------,
dt h -> 0 h dt
donde dt no es más que un paso temporal pequeño. Despejando de la fórmula de la derivada, se encuentra que, si conocemos las posiciones y velocidades iniciales y las fuerzas, podemos calcular las posiciones y velocidades nuevas después de un intervalo de tiempo dt.
v(t
+ dt)
=v(t)
+ a(t)*dt,
r(t
+ dt) =
r(t)
+ v(t)*dt,
Ahora, con las posiciones nuevas, se pueden calcular de nuevo las fuerzas. Repitiendo este proceso, se puede ir avanzando paso a paso en el tiempo calculando la trayectoria de la partícula.
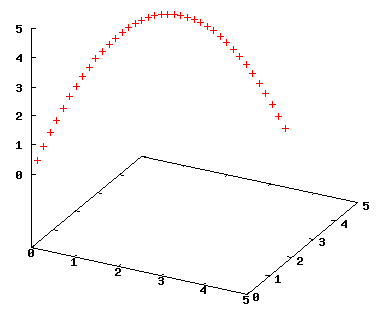
Figura 4: Trayectoria de una partícula calculada con fuerzas.bc.
En la figura 4, se puede ver la trayectoria tridimensional de una masa lanzada en un campo gravitatorio, un problema clásico de física de bachillerato. El código bc no es difícil de entender. Simplemente define los parámetros de la simulación: posiciones y velocidades iniciales, tiempos iniciales y finales, paso temporal y constantes (aceleración de la gravedad, masa y carga). A continuación define la función aceleraciones, que utiliza la segunda ley de Newton para calcular las aceleraciones a partir de las fuerzas. En general, la fuerza será una función de la posición, la velocidad, la masa y la carga. Por último, la función integra_ec integra las ecuaciones del movimiento utilizando el método de pasos temporales pequeños explicado antes y produce una lista de datos por columnas. La primera columna presenta el instante temporal y las otras tres las coordenadas rx, ry y rz. Utilizando esta lista, se representó la trayectoria de la figura 4 con el programa gnuplot.
Es muy fácil modificar el comportamiento de fuerzas.bc para simular otro tipo de fenómenos. Supongamos que queremos simular el movimiento de un oscilador amortiguado. En este caso, la segunda ley de Newton es
a = d2x/dt2 = − (k/m) x − (c/m) dx/dt.
Así que, aparte de los cambios apropiados en las condiciones iniciales, tenemos que convertir la función aceleraciones en ésta:
define aceleraciones(r[], v[], *a[], masa, carga) {
a[1] = -(k/m)*r[1] -(c/m)*v[1];
a[2] = 0;
a[3] = 0;
return 0;
}
Evidentemente, también habrá que especificar los valores de las constantes nuevas k y c.
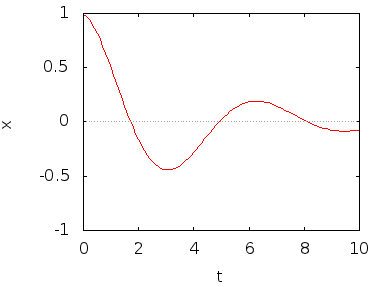
Figura 5: Elongación
frente a tiempo para un oscilador armónico
amortiguado.
En la figura 5, se puede ver la gráfica de x frente a t para un oscilador amortiguado con los siguientes valores iniciales y constantes k y c:
rx = 1, ry = rz = 0,
vx = vy = vz = 0,
k = 1, c = 0,5.
La función que integra las ecuaciones del movimiento es exactamente la misma que en el caso del lanzamiento. El lector interesado sin duda querrá ensayar con sus propias versiones para cometas, satélites o campos electromagnéticos.
Los principales problemas que puede presentar ahora la dinámica de una partícula tienen que ver con la selección de las magnitudes adecuadas (unidades y tamaño del paso de tiempo) y escribir la ecuación para la aceleración en términos de la posición y velocidad de la partícula. Pero hallar la trayectoria a partir de la ecuación se ha convertido en una tarea muy fácil.
El código fuerzas.bc presupone que sólo se está simulando el movimiento de una partícula. Sin embargo, no es muy difícil generalizar el método a un número arbitrario de partículas que interactúan. Con pasos de integración adecuados, es relativamente fácil programar un modelo numérico básico del sistema solar, por ejemplo.
4.2.2 Campos de fuerzas (campos.bc)
Si te encuentras en un examen con un problema en el que tienes que calcular el campo eléctrico creado por un hilo cargado o una superficie, o algo parecido, normalmente te pedirán que realices el cálculo para un punto en el que las operaciones se simplifican bastante a causa de la simetría de la disposición de cargas.
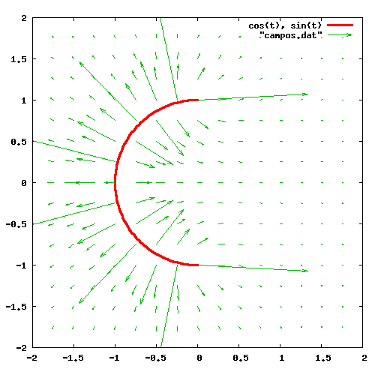
Figura 6: Campo eléctrico creado por un semicírculo cargado.
Por ejemplo, para el semicírculo cargado de la figura 6, lo habitual es pedir el campo eléctrico en el centro del arco, es decir, el punto (0, 0) de la gráfica. Pero calcular el valor del campo en otros puntos se convierte en una tarea bastante más tediosa. Evidentemente, la mayoría de las aplicaciones prácticas de la electrostática exigen conocer los campos en muchos puntos, no solo donde es fácil calcularlos.
El código de campos.bc no es más que un ejemplo de cómo hacer este tipo de cálculos. El resultado se ha representado en la figura 6 usando el programa gratuito gnuplot.
Es verdad. Todos estos cálculos se pueden hacer también aprendiendo a manejar algún programa matemático como Octave, Maxima, Maple o Mathematica. Pero para muchas cosas basta una herramienta relativamente sencilla como bc. La programación en bc tiene el encanto del bricolaje: cuando terminas, puedes mirar con satisfacción algo que has hecho tú. No hay ninguna duda de que esto tiene mucho valor desde el punto de vista didáctico, pero lo que me gustaría defender a mí es que un ordenador "viejo" no tiene por qué suponer una limitación. Evidentemente, no podrás jugar a los últimos juegos de acción sin una tarjeta gráfica potente, pero la gran mayoría de las cosas que tienes que hacer en una carrera técnica se pueden hacer con cualquier cacharro. Si a Einstein no le hizo falta tanta potencia de cálculo, probablemente tampoco la necesitarás tú.
