Métodos matemáticos I
Próximas tutorías
Martes, 19 de mayo 16:00–17:30.
Novedades
25/03/2015 En el apartado de cálculo numérico, he copiado el programa que escribí para hallar la solución numérica de una ecuación diferencial por el método de Euler y los comandos para representar un campo de pendientes en Maxima.
18/03/2015 He añadido una sección de divulgación sobre las transformaciones de Möbius y vídeos en los que se ven ampliaciones del fractal de Mandelbrot. A partir de la próxima clase nos dedicaremos a estudiar ecuaciones diferenciales.
Problemas de examen
Otros problemas de examen que merece la pena intentar:
1. a) Si z = x + iy demostrar entonces que
zz* = |z|2.
b) Utilizando los resultados del apartado anterior, y teniendo en cuenta que
z = xj + iyj (j = 1, 2) encontrar las
condiciones bajo las que se verifica que
|z1 + z2|
≤ |z1| + |z2|;
|z1 − z2|
≥ |z1| − |z2|.
2. Determinar y dibujar en el plano complejo el lugar
geométrico de los puntos que satisfacen respectivamente las
ecuaciones:
|ez2| = 1 y
|e(z − 1/z)| = 1.
3. Descomponer el polinomio z4 −
4z2 + 3 en dos factores cuadráticos y con ellos
demostrar que si |z| = 2 entonces
|1/(z4 − 4z2 + 3)| ≤ 1/3.
4. a) ¿Cuál es la diferencia entre que una función
f(z) sea derivable en un punto y que sea holomorfa (o
analítica) en ese punto?
b) Demostrar que si una función compleja es derivable en un punto entonces
debe verificar las condiciones de Cauchy-Riemann. ¿Son estas condiciones
suficientes para garantizar la derivabilidad en ese punto?
5. Dibujar la imagen del plano complejo bajo la
transformación
h(z) = i/Log(z),
donde Log(z) denota la rama principal del logaritmo (Obs: Notar que
1/Log(z) es la composición de 1/z con el logaritmo).
6. Demostrar que si a es un número complejo tal que
|a| < 1, entonces la transformación
w = (a − z)/(1 − a* z)
transforma el disco |z| < 1 en sí mismo, y la circunferencia
frontera |z| = 1 en sí misma.
7. Mostrar que para cualquier elección de las constantes
c1 y c2, la función
f(x)
= c1 e−x
+ c2 e2x
es una solución explícita de
y'' − y' − 2y = 0.
8. Resolver el problema de valor inicial
dy/dx
= (−2x + y)2 − 7,
y(0) = 0.
9. a) Encontrar la solución general de la ecuación
diferencial
dy/dx = y2x2
+ y2 + 1
+ x2.
b) Encontrar la solución que verifica la condición inicial y(0) =
1.
10. Encontrar el valor del parámetro b
en la ecuación diferencial
(xy2 + bx2y)dx
+ (x + y)x2dy = 0
para que sea una ecuación diferencial exacta y luego encontrar la
solución general de dicha ecuación para el valor de b
calculado.
11. a) Encontrar la solución general de
la ecuación diferencial
dy/dx = y2x2
+ y2 + 1
+ x2.
b) Encontrar la solución tal que y(0) = 1.
12. a) Demostrar que las funciones
y1(x) = ex,
y2(x) = e2x y
y3(x) = e3x son linealmente
independientes en el intervalo (-∞, ∞).
b) Encontrar la ecuación diferencial homogénea para la cual las funciones del
apartado a) forman un sistema completo de soluciones.
13. Encontrar la solución general de la ecuación
diferencial
d4y/dx4
− d2y/dx2
= 24x2.
14. a) Encontrar la solución general del sistema de ecuaciones diferenciales
| x1 |
| x2 |
| x3 |
| 1 | 1 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 2 |
| x1 |
| x2 |
| x3 |
utilizando exclusivamente métodos matriciales.
b) Hallar la solución cuyas condiciones iniciales son
| x1(0) |
| x2(0) |
| x3(0) |
| 1 |
| 1 |
| 1 |
Problemas resueltos en tutorías anteriores:
1. Escribir en la forma a + ib las raíces de la ecuación z3 + 1 = 0.
2. Encontrar la región del plano complejo determinada por la ecuación |z|2 ≤ 2 Re(z).
3. a) Encontrar las raíces de la ecuación
z6 + 7 z3 − 8 = 0.
b) ¿Por qué tres de ellas están sobre una circunferencia y las otras tres sobre
otra? Determinar dichas circunferencias y representar en el plano complejo-z
estas raíces.
4.
Sean z1 y z2 dos números
complejos cualesquiera. Demostrar que
|z1 + z2|
≤ |z1| + |z2|,
y
|z1 − z2|
≥ ||z1| − |z2||.
5.
Sea B = {z tales que |z| < 1}. Determinar el
conjunto
A = {z tales que |ez2| ∈
B}.
6. a) Demostrar que la función
u(x, y) = 2x −
x3 + 3xy2 es armónica en un
cierto dominio.
b) Encontrar la función armónica más general
v(x, y) de u(x, y)
y la función analítica cuya parte real es u y cuya parte
imaginaria es v.
7. Sea z = x + iy. Determinar todos los valores de log(z½) en función de x, y.
8. a) Demostrar que u(x, y) =
x3 − 3xy2 + 2y puede ser
la parte real de una determinada función analítica f(z).
b) Encontrar dicha función f(z) y la armónica conjugada de
u(x, y).
c) Si v(x, y) es la armónica conjugada de
u(x, y) y se anula en x = 0; y =
0, ¿Cuáles son los ceros de f(z)?
9. Dada una función f(z) =
u(z) + iv(z) con
u(z), v(z) ∈ ℜ
continuas en todo el plano complejo, y tal que
∂2u/∂x2 +
∂2u/∂y2 = 0,
∂2v/∂x2 +
∂2v/∂y2 = 0,
¿Podemos asegurar que f es holomorfa?
10. Dada h(z) la rama de la raíz cuarta,
con corte de ramificación {x = −y, x ≥ 0},
tal que h(1) = −1,
a) Determinar h(i) y h(−i).
b) Determinar si existen, y calcular en su caso,
limz→−1 h(z) y
limz→1−i h(z)
11. Si denotamos por Log el valor principal del logaritmo
complejo, definido en todo el plano excepto en 0,
a) Determinar los puntos en los que Log(iz2) no es
continua, determinando los límites direccionales en esos puntos (siguiendo
trayectorias rectas),
b) Para qué valores de z se tiene que Log(z2) = 2
Log(z)?
12. Determinar la imagen de
{z, |z| < 2 y Re(z) ≥ 0}
bajo la aplicación
h(z) = (iz + 2)/(z − i).
13. Dado que
y1(x) = e2x
cos(3x)
e
y2(x) = e2x
sin(3x)
son soluciones de la ecuación homogénea
y'' − 4y' + 13y = 0,
determinar una solución de esa ecuación que satisfaga las condiciones iniciales
y(0) = 5, y'(0) = 2.
14. Calcular el valor del parámetro a para que la
ecuación diferencial
(axy − 1/cos2x) dx
+ (x2 + 2y) dy = 0
sea exacta, y dar una solución general en forma implícita para ese valor de
a.
15. Determinar la solución general de la ecuación
diferencial
dy/dx = (x + y + 2)2.
16. Resolver la ecuación diferencial
dy/dx = sen(x − y).
17. Encontrar la solución general de la
ecuación diferencial
dy/dx
= (x + y + 4)/(x − y − 6).
18. Sabiendo que la ecuación diferencial
yF(x)dx
+ x2G(y)dy = 0 admite el factor
integrante μ(x, y) = ey sen x se pide:
a) Determinar las funciones F(x) y
G(x).
b) Resolver la ecuación resultante.
19. Resolver el problema de valor inicial
d2y/dx2
− 3 dy/dx + 2y
= 2e−x;
y(0) = 2;
dy/dx|x = 0 = 1.
20. Dada la ecuación diferencial
(x cos(x) - sen(x))
d2y/dx2
+ x sen(x) dy/dx
− y sen(x) = 0,
se pide:
a) Determinar una solución de ella, sabiendo que es del tipo y =
xα para un valor determinado del parámetro
α.
b) Utilizando los resultados del apartado anterior, hallar la solución general
de la ecuación diferencial propuesta y aquella solución yp
que está acotada cuando x → +∞ y además
yp(π/4) = 1.
21. Resolver el problema del valor inicial:
d3y/dx3
− 5 d2y/dx2
+ 9 dy/dx - 5y = 0;
y(0) = 0; dy/dx|x = 0 = 1;
d2y/dx2|x = 0 = 6.
22. a) Determinar la solución general del sistema de ecuaciones diferenciales:
| x1' | = | 3x1 + x2, |
| x2' | = | 2x1 + 2x2. |
b) Hacer un dibujo aproximado del diagrama de fases del sistema y clasificar el tipo de punto crítico que es el punto (0, 0).
23. Encontrar la solución general de la ecuación
diferencial
d4y/dx4 −
d2y/dx2
= 24x2.
24. Dar la solución general de la ecuación
diferencial
y''' + 3y'' − 4y
= et + e−t.
25. Determinar la solución general de la ecuación
diferencial
d2y/dt2 + y
= tan(t) + 1,
t ∈ (−π/2, π/2).
26. Resolver, usando transformadas de Laplace, el
siguiente
problema de valor inicial.
y'' + 2y' = δ(t − 1),
y(0) = 0,
y'(0) = 1,
donde δ(t) denota la función delta de Dirac.
Recursos adicionales
Si te gusta apoyarte en las clases para aprender la asignatura, las tutorías del centro asociado no son suficientes, pero tienes muchas otras a tu disposición. Busca "variable compleja" o "complex variables" en Youtube. Copio debajo dos ejemplos:
Cálculo numérico
Números complejos
Muchos programas permiten operar directamente con números complejos. Por ejemplo, yo he programado mis propias rutinas para bc (que por supuesto puedes consultar, utilizar, modificar y distribuir). Recuerda que utilizan la rama arg(z) ∈ (−π, π].
Puedes usar estos programas para comprobar tus cálculos. En física computacional te enseñan a manejar Maxima. En las tutorías vimos que (1 + i)8 = 16. Para comprobarlo, podemos escribir en Maxima lo siguiente:
(%i1) (1 + %i)^8;
8
(%o1) (%i + 1)
(%i2) expand((1 + %i)^8);
(%o2) 16
Con Maxima puedes operar de manera simbólica, lo cual te permite comprobar cosas como, por ejemplo, que zz* = |z|2.
(%i3) expand( (a + b*%i) * conjugate(a + b*%i) );
2 2
(%o3) b + a
(%i4) expand( cabs(a + b*%i)^2 );
2 2
(%o4) b + a
Más información:
- Aritmética real y compleja (José Manuel Mira Ros, Universidad de Murcia).
- Maxima: Funciones para los números complejos.
Ecuaciones diferenciales
Esta es una versión comentada del programa que escribí en la tutoría para calcular numéricamente la solución de una ecuación diferencial ordinaria de orden uno por el método de Euler.
/******************************************************************************
* Euler.bc *
******************************************************************************
Integración numérica de la ecuación diferencial ordinaria de orden 1
dy/dx = g(x, y)
utilizando el método de Euler.
Autor: Marc Meléndez Schofield.
Se permite la reproducción, distribución y modificación de este código.
/----------------------------------------------------------------------------/
Para ejecutar este programa en Unix/Linux:
bc -l Euler.bc
Para grabar los datos en un fichero, se puede hacer así:
bc -l Euler.bc > Euler.dat
La solución numérica se puede representar en gnuplot. Primer se ejecuta
gnuplot:
gnuplot
y luego se utiliza el comando:
gnuplot> plot "Euler.dat" w l
*/
/* Definición de la función g(x, y) en la ecuación diferencial */
define g(x,y) {
return 4*y*(1 - y);
}
/* Parámetros del algoritmo de integración numérica */
scale = 5; /* Número de decimales en los cálculos */
dx = 0.001; /* Paso de integración */
x0 = 0; /* Valor inicial de x */
xf = 5; /* Valor final de x */
y = 0.002; /* Valor inicial de y = y(x0) */
/* Cabecera de la tabla de datos */
print "# x \t y #\n#---\t---#\n";
/* Algoritmo de integración numérica (método de Euler) */
for(x = x0; x <= xf; x += dx)
{
y += g(x,y)*dx;
print x, "\t", y, "\n";
}
quit;
Para representar un campo de pendientes en Maxima, utilizamos los
comandos:
(%i1) load("plotdf");
(%o1) /usr/share/maxima/5.32.1/share/dynamics/plotdf.lisp
(%i2) plotdf([y,x]);
(%o2) /home/marc/maxout.xmaxima
Divulgación
El fractal de Mandelbrot
Hace unos años, me pidieron que escribiera un artículo sobre Mandelbrot que puedes encontrar siguiendo el enlace:
Mandelbrot, domador de fieras matemáticas.
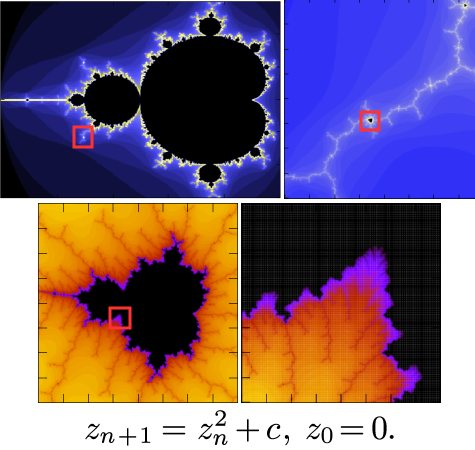
Para dibujar el fractal tenemos que calcular qué ocurre con cada punto
c del plano complejo cuando realizamos la siguiente iteración:
zn+1 = zn2 +
c, (con z0 = 0).
Pintamos de negro los puntos tales que limn→∞
|zn| < ∞.
He escrito debajo un código sencillo de bc que genera el fractal de Mandelbrot. Se apoya en mis rutinas de números complejos. Genera una lista de coordenadas x e y, junto con el color correspondiente a la coordenada. Luego se pueden utilizar estos datos para representar el fractal. Yo utilicé gnuplot.
/* Ejecutar con bc -l complejos.bc mandelbrot.bc */
scale = 20;
maxcolor = 100;
/* Calcular el color de c = x + iy */
define mandelbrot(x, y) {
zn[0] = 0;
zn[1] = 0;
c[0] = x;
c[1] = y;
for(k = 0; k <= maxcolor; k++)
{
/* El nuevo valor de zn es (zn)^2 + c */
. = prodz(zn[], zn[], zn[]); /* Cuadrado */
. = sumaz(zn[], c[], zn[]); /* Sumar c */
/* Si el módulo de zn aumenta sin límite,
se le asigna un color */
if(modz(zn[]) > 2)
return maxcolor - k;
}
/* Si el módulo sigue acotado,
dejamos un punto negro */
return 0;
}
/* Generar el fractal con 400x400 píxeles */
for(x = 0; x <= 400; x++)
{
for(y = 0; y <= 400; y++)
{
print x, " ", y, " ";
print mandelbrot(-2.0 + 3.0*x/400, 2.0*y/400 - 1.0), "\n";
}
print "\n";
}
quit;
Ampliar el fractal de Mandelbrot

En la segunda tutoría, si no recuerdo mal, dije que si amplías el fractal de Mandelbrot tanto como quieras, sigue teniendo una estructura intrincada. Un alumno me dijo que había intentado ampliar la imagen del apartado anterior. Evidentemente, en ese caso se acaban viendo sólo unos cuantos píxeles de colores. Yo me refería a ampliar la estructura matemática, no una imagen del conjunto. Debajo he incluido enlaces a vídeos donde se aplican ampliaciones verdaderamente gigantescas al fractal de Mandelbrot:
Mandelbrot Zoom 10^227 [1080x1920]
Mandelbrot fraktaler super deep 2 2^4750
A mí me encanta el último medio minuto de estos vídeos. Se ve algo realmente fascinante.
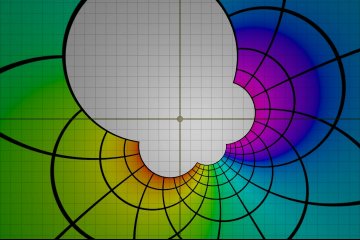
Transformaciones de Möbius y la esfera de Riemann
Durante una tutoría mencioné brevemente que las transformaciones de Möbius se podían entender desde el movimiento de la esfera de Riemann. En 2007, D. Arnold y J. Rogness crearon un cortometraje que ilustraba muy bien esta idea: Möbius Transformations Revealed.